Travaux dirigés de probabilités n°5
Exercice n°1
Un jardinier décide de semer des graines de potiron. Le pouvoir germinatif de chaque graine est de 0,8.
1) Il sème huit graines. Quelle est la probabilité que
a) Sept graines germent ? b) Au moins sept graines germent ?
2) Quand une graine a germé, la probabilité que les limaces détruisent le jeune plant est de 0,5.
a) Calculer la probabilité qu’une graine semée donne un bon plant à repiquer, c’est-à-dire que la graine germe et que les limaces ne mangent pas le jeune plant ?
b) Combien faut-il semer de graines pour que la probabilité d’avoir au moins un bon plan soit supérieure à 0,99 ?
1) a) X suit la loi binomiale (8 ; 0,8)
P (X = 7) = ![]() 0,87 0,2 = 0,336
0,87 0,2 = 0,336
La probabilité pour que sept graines germent est de 0,336
b) P (X![]() 7) = P (X = 7) + P (X = 8) =
7) = P (X = 7) + P (X = 8) = ![]() 0,87 0,2 +
0,87 0,2 + ![]() 0,88 = 0,336 + 0,168 = 0,504
0,88 = 0,336 + 0,168 = 0,504
La probabilité pour qu’au moins sept graines germent est de 0,504.
2) a) Le pouvoir germinatif de chaque graine est de 0,8. Sachant que la graine a germé, les limaces ne la mangent pas avec une probabilité de 0,5 ; donc la probabilité pour qu’une graine semée donne un plant à repiquer est de 0,8 * 0,5 = 0,4.
b) X suit la loi binomiale (n ; 0,4)
P (X![]() 1) = P (X = 1) + P
(X = 2) + … + P (X = n) = 1 – P (X = 0) = 1 -
1) = P (X = 1) + P
(X = 2) + … + P (X = n) = 1 – P (X = 0) = 1 - ![]() 0,6n =
1 – 0,6n
0,6n =
1 – 0,6n
1 – 0,6n
> 0,99![]() 0,6n
< 0,01
0,6n
< 0,01![]() n ln 0,6 < ln 0,01
n ln 0,6 < ln 0,01
ln 0,6 < 0 ![]() n >
n > ![]()
![]() n > 9,015
n > 9,015
Il faut semer au moins dix plants pour que la probabilité d’avoir au moins un bon plan soit supérieure à 0,99.
Exercice n°2
Une machine déréglée produit des pièces dont un tiers sont défectueuses. Dans un lot de neuf pièces fabriquées par cette machine, calculer le nombre moyen de pièces défectueuses et la probabilité associée. On assimilera le tirage des neuf pièces à un tirage avec remise.
X suit la loi binomiale (9, ![]() )
)
9 * ![]() = 3.
= 3.
Le nombre moyen de pièces défectueuses est de 3.
P (X = 3) = ![]()
![]()
![]() =
= ![]() *
*![]() *
*![]() =
= ![]() = 0,273.
= 0,273.
La probabilité d’avoir trois pièces défectueuses est de 0,273.
Exercice n°3
Dans la forêt équatoriale, chaque naissance de gorilles donne un gorille gaucher avec une probabilité égale à 0,3. Un gorille gaucher sur trois a les yeux bleus, un gorille droitier sur quatre a les yeux bleus.
1) Calculer la probabilité pour qu’un gorille pris au hasard ait les yeux bleus.
2) Soit X la variable aléatoire égale au nombre de gorilles gauchers aux yeux bleus parmi six naissances de gorilles dans la forêt.
a) Quelle est la loi probabilité de X ?
b) Calculer son espérance et sa variance.
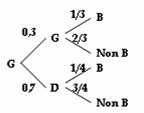
1) P (B) = 0,3 * ![]() + 0,7 *
+ 0,7 * ![]() = 0,275.
= 0,275.
La probabilité pour qu’un gorille pris au hasard ait les yeux bleus est de 0,275.
2) P (G![]() B) = 0,3 *
B) = 0,3 * ![]() = 0,1
= 0,1
X suit la loi binomiale (6 ; 0,1)
P (X = k) = ![]() 0,1k 0,96-k
0,1k 0,96-k
|
X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
P |
0,5314 |
0,3543 |
0,0984 |
0,0146 |
0,0010 |
0,0001 |
0 |
E (X) = 1 * 0,3543 + 2 * 0,0984 + 3 * 0,0146 + 4 * 0,001 + 5 * 0,0001 + 6 * 0 = 0,6 = 6 * 0,1 = n * p
V (X) = (1² * 0,3543 + 2² * 0,0984 + 3² * 0,0146 + 4² * 0,001 + 5² * 0,0001 + 6²) – 0,6² = 0,54 = 6 * 0,1 * 0,9 = n * p * (1 – p)
Exercice n°4
On vous propose le jeu suivant : vous lancez deux n fois une pièce équilibrée, vous êtes gagnant si vous obtenez autant de piles que de faces. De plus, vous pouvez choisir entre n = 3 et n = 10. Quel est le meilleur choix ?
P (G /n = 3) = ![]() 0,53 0,53 =
0,53 0,53 = ![]() 0,56 =
0,56 = ![]() * 0,56 = 0,3125.
* 0,56 = 0,3125.
P (G / n = 10) = ![]() 0,510 0,510 =
0,510 0,510 =
![]() * 0,520 = 0,176
* 0,520 = 0,176
Le meilleur choix est de choisir n = 3 pour maximiser ses chances de gagner.
Exercice n°5
Un questionnaire à choix multiples est constitué de soixante questions. Pour chaque question, quatre réponses sont possibles : une seule est juste. On suppose que le candidat choisit une et une seule réponse pour chaque question.
Chaque réponse juste rapporte trois points et chaque réponse fausse enlève un point. Pour une copie, on note :
X le nombre total de bonnes réponses.
Y le nombre total de points obtenus divisé par neuf (ce qui constitue la note du candidat).
1) Exprimer Y en fonction de X.
2) Quelle est la note d’une copie contenant exactement trente bonnes réponses ? Combien faut-il de bonnes réponses pour que la note soit au moins égale à dix ?
3) On suppose dans la suite que toutes les réponses sont faites au hasard.
Quelle est la loi de probabilité de X ? Calculer son espérance et sa variance.
4) Déterminer E(Y) et V(Y).
5) Calculer la probabilité pour que le candidat ait 20.
(on donne le résultat numérique suivant
![]() = 7,5 * 10-37)
= 7,5 * 10-37)
1) Y = [3X - (60 – X) * 1] / 9 = [3X - 60 + X] / 9 = ![]()
2) Si X = 30, Y = ![]() =
= ![]() 6,67
6,67
La note d’une copie qui a 30 bonnes réponses est de 6,67.
![]()
Il faut avoir 38 bonnes réponses pour obtenir au moins 10.
3) X suit la loi binomiale (60 ; 0,25)
P (X = k) = ![]() 0,25k * 0,7560-k
0,25k * 0,7560-k
4) E (X) = 60 * 0,25 = 15
V (X) = 60 * 0,25 * 0,75 = 11,25
5) P (X = k) = ![]() 0,2560 =
0,2560 = ![]() = 7,5 * 10-37
= 7,5 * 10-37
La probabilité d’avoir 20 est de 7,5 * 10-37.
Exercice n°6
Sur le rayonnage d’une bibliothèque se trouvent dix livres en langue étrangère : cinq en anglais, deux en allemand et trois en russe. On prélève au hasard cinq livres.
1) Calculer la probabilité que trois livres soient en anglais et deux en russe.
2) Calculer la probabilité que trois livres soient dans une langue et deux dans une autre.
3) Soit X la variable aléatoire qui, à chaque tirage de cinq livres, associe le nombre de volumes en russe. Quelle est la loi de probabilité de X ? Sa fonction de répartition ?
1) ![]() =
= 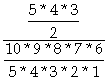 =
=![]() 0,119
0,119
La probabilité pour que trois livres soient en anglais et deux
en russe est de ![]() .
.
2) ![]() =
= 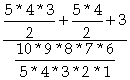 =
=![]()
La probabilité pour que trois livres soient dans une langue et
deux dans une autre est de ![]() .
.
3)
|
X |
0 |
1 |
2 |
3 |
|
P |
0,16807 |
0,36015 |
|
|
|
F |
|
|
|
|
Exercice n°7
1) Soit X une variable aléatoire suivant une loi de Poisson de paramètre 4. Déterminer p (X<8), p (X=8)
2) Soit Y une variable aléatoire suivant une loi de Poisson de paramètre 5,5. Déterminer p (4<Y<10)
Exercice n°8
Le nombre de micro-ordinateurs vendus chaque jour dans le magasin HIGHTECH suit une loi de Poisson de paramètre 4.
Calculer la probabilité que dans une journée :
1) On ne vende aucun micro-ordinateur.
2) On vende quatre micro-ordinateurs.
3) On vende au moins un micro-ordinateur.
4) Le nombre de micro-ordinateurs vendus soit compris (au sens large) entre 2 et 6.
Exercice n°9
On a constaté que 2% des ordinateurs d’un type donné tombaient en panne pour un mois d’utilisation. Une entreprise décide d’acquérir cent cinquante ordinateurs de ce type. On appelle X la variable aléatoire donnant le nombre de pannes prévisibles pour un mois, pour ce parc de cent cinquante ordinateurs (on assimilera le choix des cent cinquante ordinateurs à un tirage avec remise).
1) a) Déterminer la loi de probabilité de X.
b) Donner la probabilité des évènements suivants
- Il y a cinq pannes - Il y a au plus trois pannes.
2) a) Par quelle loi de X peut-on approcher la loi de X ?
b) Refaire les calculs du 1b avec l’approximation.
Exercice n°10
Lors d’un sondage portant sur un grand nombre d’individus, 2% des personnes interrogées acceptent de ne pas rester anonymes. Sachant que l’un des sondeurs a interrogé deux cent cinquante personnes, calculer la probabilité que :
1) Ces deux cent cinquante personnes souhaitent rester anonymes.
2) Trois personnes acceptent de ne pas rester anonymes.
3) Plus de dix personnes acceptent de ne pas rester anonymes.
Exercice n°11
Une machine à embouteiller peut tomber en panne à chaque emploi avec une probabilité de 0,01. La machine doit être utilisée mille fois. Soit X la variable aléatoire associée au nombre de pannes après mille utilisations. Les pannes sont supposées indépendantes entre elles.
1) Quelle est la loi de probabilité de X ? Calculer p(X = 0) ; p(X = 1) ; p(X > 3).
2) On estime le coût d’une réparation à 500 F. La dépense pour les réparations après 1000 utilisations est une variable aléatoire Y.
a) Estimer Y en fonction de X.
b) Calculer l’espérance et la variance de Y.
Exercice n°12
Une entreprise fabrique des pièces mécaniques. Une enquête au sein de l’entreprise a montré que 3% des pièces sont défectueuses. On tire au hasard deux cents pièces dans la production. On assimile le tirage à un tirage avec remise. On appelle X la variable aléatoire représentant le nombre de pièces défectueuses parmi les pièces tirées.
1) a) Quelle est la loi de probabilité de X ?
b) Quelles sont l’espérance et la variance de X ?
2) Par quelle loi peut-on approximer la loi de X ? Justifier.
3) Avec cette approximation, déterminer la probabilité :
a) Pour qu’il y ait huit pièces défectueuses.
b) Pour qu’il y ait au moins cinq pièces défectueuses.
c) Pour qu’il y ait au plus dix pièces défectueuses.
d) Pour que le nombre de pièces défectueuses soit compris entre trois et douze (au sens large).
Exercice n°13
1) Soit X une variable aléatoire suivant une loi binomiale de
paramètres n = 4 et p = ![]() .
.
a) Calculer p (X=0) et p (X=1).
b) Quelle est l’espérance de X ?
2) Soit Y une variable aléatoire suivant une loi de Poisson de paramètre m = 7.
a) Déterminer p (Y = 5) et p (Y = 7).
b) Déterminer p (4<Y![]() 12).
12).
c) Quelles sont l’espérance et la variance de Y ?
Exercice n°14
Le bureau d’une association est formé de six personnes. Chacune d’elles a la probabilité 0,5 d’assister à la prochaine réunion. Quelle est la probabilité que deux tiers au plus des membres de ce bureau assistent à cette réunion ?
Exercice n°15
Un candidat à un jeu télévisé doit répondre à quatre questions de type QCM. Pour chaque question, trois réponses sont proposées dont une seule est exacte. Le candidat répond au hasard.
On appelle K le nombre de réponses exactes fournies par le candidat.
1) Déterminer la loi de K.
2) On attribue trois points par réponse juste et on retire un point par réponse fausse. Combien de points le candidat peut-il espérer obtenir ?
Exercice n°16
L’agence de voyages TOUROR possède un certain nombre de villages clubs d’une capacité de trois cents places. Le taux de défection après réservation est loin d’être négligeable, puisqu’il est de l’ordre de 2%. Aussi le potentiel offert est il mal exploité car, jusqu’à maintenant, les réservations se limitaient à trois cents places et qu’aucune liste d’attente efficace n’avait pu être mise en place.
1) Donner la loi du nombre de désistements en justifiant votre réponse.
2) Par quelle loi peut-on approximer la loi trouvée ? (Justifier)
3) Donner la loi de probabilité d’avoir trois défections dans un village club puis celle d’avoir plus de cinq défections.
4) Calculer l’espérance et l’écart type du nombre de désistements.
Exercice n°17
Une équipe de football gagne son match avec une probabilité de 0,4, fait match nul avec une probabilité de 0,3 et perd avec une probabilité de 0,3. Pendant cinq semaines consécutives, elle joue un match par semaine. On suppose que les résultats des matchs sont indépendants.
Déterminer les probabilités pour que :
1) Elle gagne tous les matchs.
2) Elle ne gagne aucun match.
3) Elle gagne au moins quatre matchs.
Exercice n°18
Vous cambriolez une entreprise de jouets et repartez avec l’ensemble des mille légos fabriqués dans la journée. Arrivé dans votre parc, vous mettez tout dans votre coffre à jouets. 60% des légos ont une forme carrée, 30% sont des triangles et 10% des disques. Vous choisissez cinquante légos au hasard. Soit X la variable aléatoire représentant le nombre de légos de forme triangulaire.
1) Quelle est la loi de probabilité de X
2) Quelle est la probabilité d’avoir vingt triangles ?
Exercice n°19
Une machine produit des pièces dont 5% sont défectueuses. Soit X la variable aléatoire associant à chaque échantillon de n pièces le nombre de pièces défectueuses de cet échantillon. (le tirage est assimilé à un tirage avec remise).
1) Déterminer la loi de probabilité de X.
2) On tire au hasard avec remise un lot de dix pièces. Quelle est la probabilité pour que :
a) Il n’y ait aucune pièce défectueuse ?
b) Toutes les pièces soient défectueuses ?
Exercice n°20
Un candidat à un poste d’agent d’administration d’une entreprise passe un test de culture générale. Ce test comporte vingt questions. Chaque question comporte cinq réponses possibles ; si le candidat donne la bonne réponse, il a un point, sinon il n’a pas de point. On suppose que le candidat répond totalement au hasard aux questions et que les vingt questions sont indépendantes. Soit X la variable aléatoire représentant le nombre de points obtenus par le candidat.
1) Quelle est la loi de probabilité de X ? Calculer son espérance et sa variance.
2) Quelle est la probabilité qu’un candidat obtienne strictement plus de deux points ?
Exercice n°21
On sait que la probabilité qu’une personne soit allergique à un certain médicament est égale à 10-3. On s’intéresse à un échantillon de mille personnes. Soit X la variable aléatoire correspondant au nombre de personnes allergiques dans l’échantillon.
1) Déterminer la loi de probabilité de X.
2) En utilisant une approximation que l’on justifiera, calculer les probabilités pour que :
a) Il y ait exactement deux personnes allergiques dans l’échantillon.
b) Il y ait au moins deux personnes allergiques dans l’échantillon.
Exercice n°22
Dans une entreprise, une machine produit des pièces dont les dimensions très précises doivent être respectées.
PARTIE A : Après un premier réglage, on constate une proportion de 30% de pièces défectueuses. On examine cinq pièces choisies au hasard dans la production. Ce tirage est assimilé à un tirage avec remise. Soit X la variable aléatoire associée au nombre de pièces défectueuses parmi les cinq.
1) Quelle est la loi de probabilité de X ?
2) Calculer l’espérance et l’écart type de X.
3) Quelle est la probabilité pour que deux pièces soient défectueuses ?
4) Quelle est la probabilité pour qu’il n’y ait pas plus d’une pièce défectueuse ?
PARTIE B : Après un second réglage, la proportion des pièces défectueuses devient égale à 5%. On examine un lot de cent pièces. Soit Y la variable aléatoire correspondant au nombre de pièces défectueuses parmi les cent.
1) Quelle est la loi de probabilité de X ?
2) Par quelle loi peut-on l’approximer ?
Dans la suite des questions, on utilisera cette approximation pour faire les calculs demandés.
3) Calculer la probabilité d’obtenir deux pièces défectueuses ?
4) Calculer la probabilité pour que le nombre de pièces
défectueuses soit compris entre deux et six. (soit p(2![]() Y
Y![]() 6)).
6)).
5) Calculer la probabilité d’obtenir strictement moins de neuf pièces défectueuses.
Exercice n°23
1) On dispose d’un bassin qui contient quarante-cinq poissons : quinze gardons et trente truites. On pêche dix poissons d’un seul coup de filet et on note X la variable aléatoire qui représente le nombre de gardons pêchés.
a) Trouver la loi de probabilité de X, son espérance et sa variance.
b) Calculer la probabilité qu’il n’y ait aucun gardon dans le filet.
2) On suppose maintenant que le bassin contient quinze gardons et cent trente cinq truites. X désigne le nombre de gardons pêchés parmi les dix poissons pêchés.
a) A quelle loi obéit X ?
b) Quel est le nombre moyen de gardons pêchés ?
Exercice n°24
Lors d’un concours d’équitation, un cavalier effectue un parcours de mille cinq cents mètres à la vitesse de dix km/h et franchit sur ce parcours six obstacles indépendamment. Pour ce cavalier, la possibilité de franchir sans faut un obstacle est de deux tiers ; le passage sans faute d’un cavalier ne ralentit pas le cavalier, tandis qu’un passage avec faute lui fait perdre une minute. Soit X la variable aléatoire qui prend pour valeur le nombre d’obstacles franchis sans faute.
1) Déterminer la loi de probabilité de X.
2) Calculer l’espérance de X.
3) Soit T la variable aléatoire correspondant à la durée du parcours.
a) Exprimer T en fonction de X.
b) Déduire de 2, la durée moyenne du parcours.