Travaux dirigés de maths financières

 

Exercice n°1

Un placement financier me garantit une augmentation de mon capital de 100% en cinq ans. Quel est le taux d’intérêt annuel

a- Si l’on raisonne à intérêts simples ?

b- Si l’on raisonne à intérêts composés ?

a)   

A intérêts simples, le taux d’intérêt annuel est de 20%.

 

b)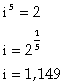 

A intérêts composés, le taux d’intérêt est de 14,9 %.

 

Exercice n°2

Si je verse 1000 euros à la fin de chaque année à un compte d’épargne à 6% d’intérêt composé annuel, quel capital aurai-je accumulé du 31.12.2000 au 1.1.2008 ?

Le capital accumulé est de 9897,47 euros.

 

Exercice n°3

On veut constituer un capital de 400 000 euros à l’aide de huit annuités constantes de fin de période. Sachant que le taux annuel de capitalisation est de 7%, déterminer le montant de l’annuité.

 


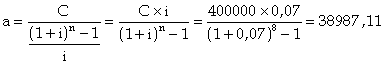
Le montant de l’annuité est de 38 987,11 euros.

Exercice n°4

Pour se constituer un capital, on place pendant 6 ans en fin d’année 25 000 euros sur un compte épargne rémunéré à 6,8 %. Quel sera le capital constitué le jour du versement de la dernière annuité ?

Le capital constitué est de 177 933,16 euros.

Exercice n°5                                                                                 

La somme de 10 000 euros placés à intérêt composé à un certain taux a produit, pendant la cinquième année de placement, un intérêt égal à celui qu’elle aurait produit, à intérêt simple, au même taux, en 427 jours. On considère qu’une année comprend 365 jours.

a- Calculer le taux de placement

b- Calculer les intérêts produits au bout de dix ans de placement.

c- A quel taux aurait-il fallu placer ce capital à intérêts simples pour rapporter les mêmes intérêts au bout de dix ans ?

a) IC5 = C5 – C4 = 10000 * (1+a)5 – 10000 * (1+a)4 = 10000 [1+a)5 – (1+a)4] = 10000 (1+a)4 (1+a-1) = 10000 a (1+a)4

Is = 10000 a

Or IC5 = Is donc 10000 a (1+a)4 = 10000 a donc (1+a)4 =

A = 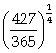- 1 = 0,04

Le taux d’intérêt est de 4%.

 

b) IC10 = C10 – Ci = C (1 + i)n – C = C [(1 + i)n – 1]

IC10 = 10000 [(1 + 0,04)10 – 1] = 4802,44n

Les intérêts produits au bout de 10 as sont de 4802,44 €

 

c)

Il aurait fallu placer la somme à 4,80 %.

Exercice n°6

Un capital est placé à intérêts composés pendant 5 ans : On désigne par Ck la valeur acquise par le capital à la fin de l’année k.

Sachant que C + C1 = 125 700 € et que C4 + C5 = 180 714 €

Calculer le taux de placement et le capital placé.

C + C1 = C + C (1 + i) = C (1 + 1 + i) = C (2 + i) = 125 700 €

C4 + C5 = C (1 + i)4 + C (1 + i)5 = C (1 + i)4 (1 + 1 + i) = C (2 + i) (1 + i)4 = 180 714 €

(1 + i)4 =

I = 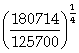- 1 = 0,04

Le taux d’intérêt est de 4%

Exercice n°7

Un emprunt de 150 000 € est remboursé sur cinq ans par annuités constantes au taux d’intérêt composé de 10%. Valeur de l’annuité ?

L’annuité est de 39 569,32 €.

Exercice n°8

Pour se constituer un capital une personne avait placé, chaque année, à partir du 1.1.90 au 1.1.99 une somme a1 au taux de 9% (composé). La valeur ainsi acquise était restée placée à intérêts composés jusqu’au 1.1.2005. A cette date, le propriétaire retirait le capital pour le prêter à une société qui acceptait de la rembourser en 10 ans, le 1er versement étant effectué le 1.1.2006, l’annuité étant a2, le taux 9%

a- Trouver a2 / a1

a) C99 = a1

C05 = (1 + i)6 * C99 = (1 + i)6 * a1 *

C05 = a2 = (1 + i)6 * a1 *

a2 = (1 + i)6 * a1 *

= (1 + i)6 *

= (1 + i)6 *

= (1 + i)16

b) a1 = = = 15 000 €

La somme ayant été placée a été de 15 000 €.

c) C05 = (1 + i)6 * a1 *= 382 801 €

La Valeur acquise au 1.1.2005 est de 382 801 €.

Exercice n°9

On veut constituer un capital de 400 000 euros à l’aide de versements égaux de 28200 € capitalisés au taux annuel de 7,56 %. Combien faudra-t-il d’annuités ?

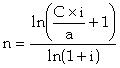
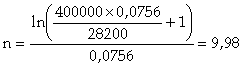
Il faut dix annuités pour se constituer ce capital de 400 000 euros.

 

Exercice n°10

On veut constituer un capital de 400 000 euros à l’aide de 7 annuités de 39 000 euros versées à terme échu. Quel est le taux de capitalisation ?

C = a

On trouve une valeur voisine de 0,125343 soit 12,5343 %. (Résultat obtenu à partir d’un tableur avec A1 valeur du taux d’intérêt et B1 = 400/39-(PUISSANCE(A1+1;7)-1)/A1 ).

 

Exercice n°11

Pour un achat on vous propose deux modes de paiement :

15 mensualités à terme échu de 800 euros chacune

12 mensualités de début de période de 1 000 euros chacune.

Quel mode doit-on choisir sachant que le taux d’intérêt annuel équivalent est de 12% ?

ia = 12% => im = - 1 = 0,009488792934582974126355069193 = 0,94888 %

C1 = 800= 11 136,04 €

C2 = a + a = 11 398,66 €

On a plutôt intérêt à choisir la première alternative, puisque on rembourse finalement moins, même si la somme peut apparaître comme la même.

 

Exercice n°12

Pour l’achat d’une machine-outil, un industriel doit verser 8 annuités de 1600 euros en fin d’année. S’il souhaitait s’acquitter de sa dette actuellement, combien devrait-il verser ? Choisir un taux annuel d’actualisation de 8%, puis de 11%.

C = 1600= 9 194,62 €

 

C = 1600= 8 233,80 €

 

Exercice n°13

Un emprunt de 10 000 euros au taux annuel de 11% est remboursé en 10 annuités constantes, la première ayant eu lieu un an après la date d’emprunt.

Montant d’une annuité ?

Quelle est la part des intérêts et celle de l’amortissement du capital dans la première annuité ?

C = a

a = = 1698,01 €

Le montant de l’annuité est de 1698,01 €.

 

a1 = Cremboursé + Intérêt = 10 000 * 0,11 + Amortissement

Amortissement = 1698,01 – 1100 = 598,01 €.

La part des intérêts est de 1100 € et celle de l’amortissement 598,01 €.

 

Exercice n°14

On emprunte 100 000 euros au taux annuel de 11,75 %. Le remboursement se fait en 10 annuités égales sans différé. Construire le tableau d’amortissement.

C = a

a = = 17517,68 €

 

Capital du

 Annuité

 Intérêt

 Amortissement

            100 000,00 €

              17 517,68 €

              11 750,00 €

                 5 767,68 €

              94 232,32 €

              17 517,68 €

              11 072,30 €

                 6 445,38 €

              87 786,94 €

              17 517,68 €

              10 314,97 €

                 7 202,71 €

              80 584,22 €

              17 517,68 €

                 9 468,65 €

                 8 049,03 €

              72 535,19 €

              17 517,68 €

                 8 522,88 €

                 8 994,80 €

              63 540,39 €

              17 517,68 €

                 7 466,00 €

              10 051,68 €

              53 488,71 €

              17 517,68 €

                 6 284,92 €

              11 232,76 €

              42 255,95 €

              17 517,68 €

                 4 965,07 €

              12 552,61 €

              29 703,35 €

              17 517,68 €

                 3 490,14 €

              14 027,54 €

              15 675,81 €

              17 517,68 €

                 1 841,91 €

              15 675,77 €

 

Exercice n°15

On emprunte 550 000 euros que l’on rembourse en 15 annuités égales sans différé, chacune d’un montant de 75 000 euros. Quel est le taux d’intérêt ?

C = a

 =

 = = = 7,33

On trouve une valeur voisine de 0,106467085 (Résultat obtenu à partir d’un tableur avec A1 valeur du taux d’intérêt et B1 = =22/3-(1-PUISSANCE(A1+1;-15))/A1 ).

 

Exercice n°16

Quelle somme constante dois-je placer tous les ans du 31/12/2001 au 31/12/2006 inclus pour disposer de 40000 euros le 1/1/2008 ? Le taux de placement est de 8,8 % et l’intérêt est composé annuellement. De quel somme disposerai-je réellement le 1/1/2008 si un prélèvement fiscal de 18,1 % a lieu sur les intérêts ?

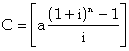* (1 + i)n

= 5668,78 €

L’annuité est de 5 668,78 €.

 

i = 40 000 – 5668,78 * 5 = 11 656, 10 €

T = i * ti = 11 656,10 * 0,181 = 2109,75 €

C = 40000 – 2109,75 = 37890,25 €

On ne disposera que de 37 890,25 € en cas de prélèvement fiscal sur les intérêts.

 

Exercice n°17

Un emprunt est remboursable par dix annuités égales versées en fin de période. Le premier amortissement est de 1560 € et le second est de 1747,20 €. Trouver le taux de l’emprunt, le montant de l’annuité, le capital emprunté.

C = a

a1 = amort1 + int1 = 1560 + C * i

a2 = amort2 + int2 = 1747,20 + (C – 1560) * i

a1 = a2 => 1560 + C * i = 1747,20 + (C – 1560) * i

C * i – (C – 1560) * i = 1747,20 - 1560

i (C – C + 1560) = 187,20

i = 12 %

 

1560 + 0,12 a= a

0,12 a – a = -1560

a (1 - 0,12 ) = 1560

a = =  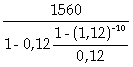= 4845,12 €

 

C = a= 27376,03 €

 

Le taux d’intérêt est de 12 %, le montant de l’annuité 4845,12 €, et le capital emprunté 27376,03 €.

 

Exercice n°18

Une banque accorde un prêt de 10 000 euros remboursable sur dix ans au taux annuel de 10 %

a) Calculer le montant de l’annuité.

b) Le client décide de rembourser son emprunt en totalité au bout de 6 ans. Quel est le montant du capital du ?

c) La banque décide de majorer le montant du capital dû de 3%. Quel est le coût total de l’emprunt ?

a) C = a

a = = 1627,45 €

Le montant de l’annuité est de 1627,45 €.

 

b) C = 1627,45 = 7 087,97 €.

Le client a remboursé au bout de six ans 7 087,97 €, donc il doit 2 912,03 €.

 

c) Coût = 6a + 2912,03 * 1,03 – 10000 = 2764,09 €

Le coût total du crédit est de 2764, 09 €.

 

Exercice n°19

L’entreprise E décide d’investir 250 000 euros dans un projet industriel. 2 modes de financement sont possibles :

1er mode : Versement d’une somme S au moment de l’achat puis versements de cinq annuités constantes égales à 60 000 euros à la fin de chaque année. Taux d’intérêt de 11,5 %. Calculer S.

2ème mode : Versement de semestrialités constantes pendant cinq ans au taux d’intérêt annuel de 11,5 %. On prendra un taux semestriel équivalent au taux annuel. Calculer le montant d’une semestrialité.

a) C = a= 60000= 218 992,67 €

S = 250 000 – 218 992,67 = 31 007,33 €

La somme versée au départ est de 31 007,33 €

 

b) is = 1,115 0,5 – 1 = 5,59 %

Le taux d’intérêt semestriel est de 5,59 %.

a = = = 33 310,27 €

Le montant d’une semestrialité est de 33 310,27 €.

 

Exercice n°20

Construire le tableau d’amortissement d’un emprunt de 50 000 euros au taux annuel de 9,5 % remboursable en cinq annuités constantes (la première annuité est payée un an après la date d’emprunt).

a = = = 13 021,82 €

Le montant de l’annuité est de 13 021, 82 €.

 

 

Capital du

Annuité

Intérêt

Amortissement

50 000,00 €

 13 021,82 €

  4 750,00 €

   8 271,82 €

 41 728,18 €

 13 021,82 €

  3 964,18 €

   9 057,64 €

 32 670,54 €

 13 021,82 €

  3 103,70 €

   9 918,12 €

 22 752,42 €

 13 021,82 €

  2 161,48 €

 10 860,34 €

 11 892,08 €

 13 021,82 €

  1 129,75 €

 11 892,07 €

 

Exercice n°21

Une entreprise hésite entre deux machines A et B

 

A

B

achat initial

100 000 euros

55 000 euros

durée de vie

10 ans

5 ans

valeur résiduelle

0

5 000 euros

 

La machine A permet un profit annuel de 16 000 euros. La machine B permet un profit annuel de 7 500 euros.

1) Calculer le taux de rentabilité interne de A. Doit-on acheter cette machine si elle est financée par un emprunt à 12 % pendant dix ans ?

2) Pour un taux d’actualisation de 12 % quelle machine doit-on préférer au regard du bénéfice actualisé ?

1)

 

Exercice n°22

Une entreprise envisage l’achat d’équipements pour moderniser les conditions de production. Deux projets lui sont proposés :

 

projet 1

projet 2

Coût initial

250 000 euros

425 000 euros

Durée d’utilisation

5 ans

5 ans

Recettes nouvelles attendues

80 000 euros par an

125 000 euros par an

Choisir l’investissement le plus rentable compte tenu d’un taux d’actualisation de 12 % et du fait que la valeur résiduelle du projet au bout des 5 ans est supposée nulle.

 

Exercice n°23

L’investissement nécessaire à réaliser le projet de Mr X suppose une dépense immédiate de 60 000 euros. Il prévoit qu’il réalisera la première année un bénéfice de 16 000 euros, la deuxième année un bénéfice de 28 000 euros, et la troisième année un bénéfice de 22 000 euros. A la fin de la troisième année, il revendra 10 000 euros son équipement.

VAN du projet ? On utilisera un taux d’actualisation de 8,5 % l’an. Mr X doit-il réaliser son projet ?

 

Exercice n°24

Un investissement d’une durée de deux ans coûte 1000 et rapporte deux fois 600 (investissement de valeur résiduelle nulle). Déterminer son TIR.

 

Exercice n°25

Un projet d’investissement d’une durée de 3 ans représente une dépense immédiate de 15 000 euros. Il rapportera trois fois 6 000 euros et la valeur résiduelle à l’issue des trois ans est supposée nulle.

TIR ? Soit i le taux annuel d’actualisation. A quelle condition le projet d’investissement est-il rentable ?

 

Exercice n°26

Soient deux projets d’investissement P1 et P2 qui représentent tous deux une dépense de 2 500 euros l’année 0. Pour le projet P1, les retours attendus sont de 1 000 euros les trois années suivantes. Pour le projet P­­2, les retours attendus sont de 800 euros l'année 1, 1430 euros l'année 2, 769 euros l’année 3.

1) Calculer le VAN de chaque projet.

a) Pour un taux d’actualisation i = 5 %  b) Pour un taux d’actualisation i = 10 %

2) On pose x = 1 + i. Soit f(x) = VAN1(X) – VAN2(X)

a) Etudier le signe de x3 f(x)

b) En déduire les positions respectives des courbes donnant la VAN de chaque projet.

3) Quel projet doit-on choisir ?

 

Exercice n°27

1) Votre banquier vous propose pour un placement d’un montant de 10 000 euros fait le 1/1/2001 au taux d’intérêt annuel de 10 % auquel s’ajoute une prime constante de 500 euros versée au 1er janvier de chaque année à partir du 1/1/2002. On appelle C0 la valeur du placement initial et Cn la valeur acquise au bout de n années.

Exprimer Cn+1 en fonction de Cn. En déduire la forme générale des termes de la suite (Cn).

2) Un concurrent propose pour le même placement de 10 000 euros un taux d’intérêt annuel de 13 %. On appelle C’0 = C0 la valeur du placement initial et C’n la valeur acquise au bout de n années. Quelle est la forme générale des termes de la suite C’n ?

3) Votre banquier affirme que son placement est plus avantageux que celui de son concurrent. Il en donne pour preuve la comparaison de C3 et C’3 puis celle de C5 et de C’5.

a) Ces deux comparaisons sont elles en sa faveur ?

b) Cela justifie-t-il pour autant son affirmation ?

 

Exercice n°28

Un particulier disposant d’un capital de 64 375 euros au 1/1/2001 décide de le prêter à une société qui lui remboursera par annuités constantes égales à 7200 euros, le taux annuel étant de 9,5 %, la première annuité étant versée le 1/1/2002.

Nombre total d’annuités versées ? (On arrondira à l’entier inférieur le plus proche).

Calculer le montant de la somme qu’il faudra ajouter à la dernière annuité pour que le capital prêté soit entièrement remboursé.

                         

Exercice n°29

Un industriel utilise des prises péritel. Pour 450 000 euros il peut acquérir une machine-outil entièrement automatique dont il attend un profit annuel de 60 000 euros. Son analyste financier estime le taux annuel d’actualisation à 5,6%.

Si le marché de la prise péritel reste non saturé, quel est le nombre d’années n nécessaires à partir duquel l’investissement devient rentable ?

Quel est l’effet d’une augmentation du taux d’actualisation sur le délai de récupération n ?

 

Exercice n°30

Pour acheter une voiture, un particulier emprunte 15 000 euros à la banque à un taux composé annuel de 8,5% remboursable par mensualités constantes de fin de période.

1) Calculer le taux mensuel équivalent.

2) Les ressources de ce particulier ne lui permettent pas de rembourser plus de 500 euros par mois. En accord avec le prêteur, il verse cette somme chaque mois et ajuste sa dernière mensualité pour payer sa dette.

a) Déterminer le nombre de mensualités nécessaires pour rembourser son emprunt.

b) Quel est le montant de la dernière mensualité ?

 

Exercice n°31

Un emprunt est remboursable par annuités constantes de fin de période.

Soit Mk le k-ième amortissement.

Sachant que M3 + M7 = 54 620,63 € et 2 M3 – M7 = 9 051,67 €

1) Calculer

a) Le taux i annuel d’emprunt.

b) L’annuité constante a sachant que le dernier amortissement est de 41 892,60 €

c) Le nombre d’annuités n

d) Le montant de l’emprunt C.

2) Faire le tableau d’amortissement.

 

Exercice n°32

Une banque prête à un pays en voie de développement un montant de cinq cent millions de dollars à un taux annuel composé de 14% remboursable en dix ans. Le remboursement se fait par annuités constantes, la première annuité étant versé un an après la date de prêt. Au bout de trois ans (après avoir versé sa troisième annuité) le pays emprunteur ne peut plus faire face au remboursement du prêt. La banque propose un rééchelonnement de la dette selon les modalités suivantes : taux d’intérêt réduit à 10%, amortissements annuels constants pendant dix ans, la première nouvelle annuité étant versée deux ans après la dernière ancienne annuité.

Au bout de cinq ans de ce nouvel échéancier, les difficultés du pays s’aggravant, il est décidé que le capital restant dû et les intérêts ne seront pas remboursés.

Construire le tableau d’amortissement. Quel capital restait dû par le pays ?

 

Exercice n°33

Compléter le tableau d’amortissement d’un emprunt dans les deux cas suivants

 

k

Ck-1

Ik

Mk

ak

1

 

 

4000

5440

2

 

 

 

 

3

 

 

 

 

 

(La première  annuité est versée un an après la date d’emprunt, i est le taux annuel d’intérêt composé, k désigne le numéro d’année, Ck désigne le capital restant du après le paiement de la k-ième annuité ak ; Mk désigne l’amortissement contenu dans l’annuité ak ; Ik désigne l’intérêt contenu dans l’annuité ak).

1) Cas où les amortissements sont  constants Mk = M

2) Cas où les annuités sont constantes ak = a

 

Exercice n°34

On considère un emprunt remboursable par amortissements constants (les annuités forment une suite arithmétique). La première annuité a1 est égale à 800 euros ; la troisième annuité a3 est égale à 770 euros ; la somme des annuités est égale à 13150 euros.

Déterminer la durée n (en années) du prêt sachant que n<30, le montant C du capital emprunté, le taux d’intérêt annuel composé i utilisé.

 

Exercice n°35

Suite à un accident une personne a obtenu une rente compensatoire de 1 600 euros par an. Chaque annuité est versée à année échue.

1) Exprimer la valeur actuelle de l’ensemble des cinq premières annuités puis de l’ensemble des n premières annuités.

2) On considère que la valeur actuelle d’une rente perpétuelle s’obtient par la limite quand n tend vers de la valeur actualisée des n premiers versements. Donner la valeur actuelle de la rente étudiée ci-dessus.