Travaux dirigés de maths

Exercice n°1

1) On donne les matrices A = et B =

Calculer AB, BA, A² - B², (A-B) (A+B). Commenter.

2) Soient les matrices A = B = C = . Calculer AB et AC. Commenter.

3) Déterminer les matrices 2.2 qui commutent avec .

1) AB = =

BA = =

A² - B² = -= - =

(A-B) (A+B) = - += =

ABBA et A² -- B² (A-B) (A+B). Donc A et B ne commutent pas.

2) AB = =

AC = =

La multiplication d’une matrice par deux matrices distinctes peut mener au même résultat.

3) Il faut trouver les matrices telles que

=

Les matrices 2.2 qui commutent avecsont de la forme

Exercice n°2 : Calculs de produits matriciels

Trouver et effectuer tous les produits réalisables de deux matrices parmi :

A = B = C = D = E =

AB = =

AC ==

AD = =

BC = =

BD = =

CA = =

DE = =

EB = =

EC = =

ED ==

Exercice n°3 : Calcul de la puissance nième d’une matrice 2*2

1) Soit la matrice. Calculer A², A³ et en déduire Aⁿ pour tout nN*

2) Mêmes questions pour les matrices B = où a est un réel.

1) A² = = A³ = =

On veut montrer que Aⁿ = pour n1

Vérifions que la propriété est vraie pour n=1

A¹ = A = . Donc la propriété est vraie pour n=1

Supposons que la propriété Aⁿ = est vraie pour n1. Montrons qu’elle est vraie pour n+1.

Aⁿ⁺¹ = Aⁿ * A==

Donc la propriété est vraie pour n+1. Donc la propriété Aⁿ = est vraie pour tout n1.

2) B² = = B³ = =

On veut montrer que Bⁿ = pour n1

Vérifions que la propriété est vraie pour n=1

B¹ = B = . Donc la propriété est vraie pour n=1

Supposons que la propriété Bⁿ = est vraie pour n1. Montrons qu’elle est vraie pour n+1.

Bⁿ⁺¹ = Bⁿ * B==

Donc la propriété est vraie pour n+1. Donc la propriété Bⁿ = est vraie pour tout n1.

Exercice n°4 : expression d’une forme quadratique

Soit le polynôme de variables réelles p(x, y, z) = 3x² + 5y² - z² - 2yx + 4xz – 3yz (appelé forme quadratique : nom donné à un polynôme de degré 2 par rapport à l’ensemble de ses variables). Trouver une matrice carrée A d’ordre 3 symétrique telle que

p(x,y,z) = ^tX.A.X où X =

Exercice n°5 : Calcul de la puissance n-ième d’une matrice carrée

Soit A =

1) Ecrire A sous la forme B+I où I est la matrice identité d’ordre 2 et B une matrice qu’on déterminera.

2) Calculer B², B³. En déduire Bⁿ pour tout n2 (par récurrence).

3) Déduire des deux questions précédentes l’expression de Aⁿ (pour nN*) en fonction de n, I, B (on pourra utiliser la formule du binôme …)

1) A = B + I

B = A – I

B = - =

2) B² = = = 0₂

B³ = B² * B = 0₂ * B = 0₂

On veut montrer que Bⁿ = 0₂ pour n2

Vérifions que la propriété est vraie pour n=2.

B² = = 0₂. La propriété est vraie pour n=2.

Supposons que Bⁿ = = 0₂. Montrons que Bⁿ⁺¹ = = 0₂.

Bⁿ⁺¹ = Bⁿ * B = 0₂ * B = O₂.

Donc la propriété est vraie pour n+1. Donc la propriété Bⁿ = 0₂ est vraie pour tout n2

3) Aⁿ = (B+I)ⁿ = = B⁰ Iⁿ + B I^n-1 + B² I^n-2 + … + Bⁿ I⁰

Or on sait que Bⁿ = 0₂ pour tout n2 donc :

Aⁿ == B⁰ Iⁿ + B I^n-1 = I + nB = + n

Exercice n°6 : un exemple de calcul de l’inverse d’une matrice 3*3

Soit B =et I la matrice identité d’ordre 3.

Calculer B² puis B² - 3B + 2I. En déduire que B est inversible. Donner l’expression de B^-1 en fonction de B et I. Ecrire explicitement B^-1.

B² ==

B² - 3B + 2I = - 3+ 2= = 0₃

B² - 3B + 2I = O₃

B² - 3B = -2I

B (B - 3I) = -2I

B (-0,5 B + 1,5 I) = I

Donc B est inversible.

B^-1 = -0,5 B + 1,5 I = + =

Exercice n°7

Soit A =

1) Trouver toutes les matrices B de la forme B = (où a, b, c sont des réels)

Telles que AB = O₃

2) Déduire de la question précédente que A n’est pas inversible ainsi que les matrices B. (Pour cela on supposera que l’inverse existe et on arrivera à une absurdité).

1) =

Donc B est de la forme

Exercice n°8

Soit la matrice d’ordre 3 définie par C =

1) Calculer C³ – 3C – 2I où I est la matrice identité d’ordre 3.

2) En déduire que C est inversible. Donner l’expression de C^-1 en fonction de I et de C. Donner explicitement C^-1.

1) C² = =

C³ = =

C³ – 3C – 2I =- 3- 2== 0₃

2) C³ – 3C – 2I = 0₃

C (C² - 3I) = 2I

C (0,5 C² - 1,5I) = I

C^-1 = 0,5 C² - 1,5I

C^-1 = 0,5- 1,5 =

Exercice n°9

Soit M_a =

1) Montrer que M_aM_b = M_a+b

2) En déduire que M_a est inversible.

3) Calculerpour tout nN (par récurrence).

1) M_aM_b = = = M_a+b

2) M_a inversible M_aM_b = I₃ = a + b = 0 b = - a

Ma est inversible et son inverse est M_-a.

3) On suppose= pour tout nN.

Vérifions que la propriété est vraie pour n = 0

=. La propriété est vraie pour n = 0.

Supposons la propriété vraie pour n. Montrons qu’elle est vraie pour n+1

=*==

Donc la propriété est vraie pour n+1. Donc elle est vraie pour tout nN.

Exercice n°10

Soit la matrice A = . Calculer A², A³.

Montrer qu’il existe 3 réels x,y,z tels que A³ = x I + y A + z A². Déduire que A est inversible et calculer A^-1.

A² = =

A³ = =

A³ = x I + y A + z A² = x+ y+ z

= x+ y+

= x+ y

A³ = -28I + 7A + 4A² A³ - 7A - 4A² = 28IA (A² - 4A – 7I) = 28IA((A² - 4A – 7I)) = I

A^-1 =(A² - 4A – 7I) =(- 4- 7) =

Exercice n°11

Soit A =

Où chaque a_ij de la matrice représente la proportion d’ouvriers travaillant au début de l’année sur la chaîne de montage j et qui travailleront l’année suivante sur la chaîne de montage i.

1) Interpréter le 0 de A.

2) Calculer A².

3) Soit X = où x_i est le nombre d’ouvriers travaillant sur la chaîne i. Que représentent AX et A²X ? Si X = . Quelle est la répartition des ouvriers dans deux ans ?

4) On donne A =  ; Calculer les puissances de A. Conclure quant à la mobilité du personnel.

1) Aucun ouvrier travaillant sur la chaîne 3 cette année n’y travaillera l’an prochain.

2) A² = =

3) AX représente le nombre d’ouvriers travaillant sur chaque chaîne l’année a+1.

A²X représente le nombre d’ouvriers travaillant sur chaque chaîne l’année a+2.

A²X = =

4) A = A² = A³ =.

Tous les deux ans, le personnel réintègre la place qui était la sienne deux ans auparavant. Il n’y a pas de mobilité au sein de cette entreprise.

Exercice n°12 : Evolution d’un système économique

1) On donne les matrices suivantes B = et P =

Calculer l’inverse P^-1 de P. Calculer A = PBP^-1. Calculer Bⁿ pour tout nN (par récurrence). En déduire une façon de calculer Aⁿ.

2) Deux comptes financiers a et b sont manipulés de la manière suivante : à la fin de chaque année 10 % du montant du compte a est versé sur le compte b et 40 % du montant du compte b est versé sur le compte a. Mis à part ces mouvements, il n’y a ni apport ni retrait sur les comptes.

S’il y avait au départ un million d’euros sur le compte a et dix millions d’euros sur le compte b, combien contiendront-ils dans deux ans ? dans dix ans ? (on prendra comme unité le million et on arrondira les résultats à 3 chiffres après la virgule.)

1) P = det P = ad – bc = 0,8 + 0,2 = 1

P^-1 =

A = PBP^-1 ===

B⁰ = B¹ = B² =

On suppose que Bⁿ = .

Vérifions que la propriété est vraie pour n = 0

B⁰ =donc la propriété est vraie pour n = 0. On suppose la propriété vraie pour n.

Montrons que la propriété est vraie pour n+1.

Bⁿ⁺¹ = Bⁿ * B ==.

Donc la propriété est vraie pour n+1. Donc elle est vraie pour tout nN.

Aⁿ = (PBP^-1)ⁿ = (PBP^-1PBP^-1)^n-1 = (PBBP^-1)^n-1 = (PB²P^-1)^n-1 = (PB³P^-1)^n-2 = … = PBⁿP^-1

On suppose que PBⁿP^-1 = Aⁿ

Vérifions que la propriété est vraie pour n=1. A = PBP^-1 donc la propriété est vraie pour n = 1.

On suppose la propriété vraie pour n.

Montrons qu’elle est vraie pour n + 1.

Aⁿ⁺¹ = Aⁿ * A = PBⁿP^-1PBP^-1 = PBⁿBP^-1 = PBⁿ⁺¹P^-1.

Donc la propriété est vraie pour n+1. Donc elle est vraie pour tout nN*.

2) A²X = PB²P^-1X ==

= =

A¹⁰X = PB¹⁰P^-1X

=== =

Exercice n°13

La population est divisée en deux catégories :

A : les personnes ayant fait des études supérieures.

B : les personnes n’ayant pas fait d’études supérieures.

D’une génération à la suivante, la mobilité d’une catégorie vers l’autre est exprimée en pourcentages dans le tableau suivant :

	A	B
A	80	20
B	60	40

(on doit lire 60 % de la catégorie B passe, à la génération suivante, dans la catégorie A).

On suppose que cette évolution reste stable de génération en génération et que pour la génération initiale, les parts de chaque catégorie sont respectivement a₀ = 5% et b₀ = 95%.

Soient a_n et b_n les parts des catégories A et B à la nième génération.

1) Exprimer matriciellement a_n+1 et b_n+1 en fonction de a_n et de b_n : = M

2) En déduire l’expression matricielle de a_n et b_n en fonction de a₀ et de b₀.

3) Soit P = . Inverser P. Puis calculer la matrice D définie par D = P^-1MP.

4) Utiliser ce résultat pour exprimer Mⁿ en fonction de P, P^-1, Dⁿ.

En déduire les expressions de a_n et b_n en fonction de n.

Si n tend vers l’infini (ce qui dans la pratique sera n10), que devient ce résultat ? Interpréter.

1) a_n+1 = 0,8 a_n + 0,6 b_n b_n+1 = 0,2 a_n + 0,4 b_n

=

2) =

3) P = . Det P = -3 – 1 = -4

P^-1 = =

D = P^-1MP ===

4) D = P^-1MP =PD = MPPDP^-1 = MM = PDP^-1

M = PDP^-1

M² = M*M = (PDP^-1)*(PDP^-1) = PD²P^-1

On suppose que Mⁿ = PDⁿP^-1

Vérifions que la propriété est vraie pour n = 1. M = PDP^-1

La propriété est vraie pour n = 1

On suppose Mⁿ = PDⁿP^-1 vraie pour n.

Montrons que Mⁿ⁺¹ = PDⁿ⁺¹P^-1 est vraie

Mⁿ⁺¹ + Mⁿ * M = PDⁿP^-1 * PDP^-1 = PDⁿDP^-1 = PDⁿ⁺¹P^-1

La propriété est vraie pour n+1 donc elle est vraie pour tout nN*.

Donc Mⁿ = PDⁿP^-1

== =

a_n = (0,75 + 0,25 * 0,2ⁿ) a₀ + (0,75 – 0,75 * 0,2ⁿ) b₀

b_n = (0,25 – 0,25 * 0,2ⁿ) a₀ + (0,25 + 0,75 * 0,2ⁿ) b₀

Exercice N°14

Sur un marché, deux produits A et B sont en concurrence (par exemple deux lessives). D’une année sur l’autre 60 % de la clientèle de A reste fidèle à A tandis que 30 % de la clientèle de B passe à A. Il n’y a pas de fuite de clientèle vers d’autres produits concurrents ni abandon de consommation de ces produits.

Soit P₀ = les parts de clientèle de A et de B en 2000 d’une façon générale

Soit P_n = les parts de clientèle de A et de B en 2000 + n (les parts de clientèle étant toujours comprises entre 0 et 1).

1) Exprimer P₁ en fonction de P₀. Traduire matriciellement cette relation sous la forme P₁ = M P₀

2) Calculer M². Utiliser ce résultat pour évaluer les parts de clientèle de A et B en 2002.

3) (DIFFICILE. FACULTATIF) Vérifier que Mⁿ – M^n-1 = (0,3)^n-1 (M-I) pour n2. En déduire le comportement de Mⁿ quand n tend vers .

1) P₁ =

2) M = M² =

P₂ =

3) On suppose que Mⁿ – M^n-1 = (0,3)^n-1 (M-I).

Vérifions que la propriété est vraie pour n = 2

M² - M – (0,3)¹ (M-I) = -- 0,3 =-+= 0₂.

La propriété est vraie pour n = 2.

On suppose que la propriété est vraie pour n.

Montrons qu’elle est vraie pour n+1

Mⁿ – M^n-1 - (0,3)^n-1 (M-I) = 0

M (Mⁿ – M^n-1 - (0,3)^n-1 (M-I)) = 0

Mⁿ⁺¹ – Mⁿ = (0,3)^n-1 (M-I) M

(M-I) M = == 0,3 = 0,3 (M-I)

Mⁿ⁺¹ – Mⁿ = (0,3)^n-1 0,3 (M-I) = (0,3)ⁿ (M-I)

Donc la propriété est vraie pour n+1 donc elle est vraie pour tout n2

Mⁿ – M^n-1 = (0,3)^n-1 (M-I)

M^n-1 – M^n-2 = (0,3)^n-2 (M-I)

M² - M = (0,3) (M-I)

Mⁿ – M = (0,3 + 0,3² + … + 0,3^n-2 + 0,3^n-1) (M-I)

Mⁿ – M = 0,3(M-I) =(M-I)

Mⁿ = 0,3(M-I) + M

Exercice n°15

Soit la matrice M =.

Déterminer la famille des matrices X telles que MX soit une matrice diagonale.

Les matrices X telles que MX soit une matrice diagonale sont de la forme

Exercice n°16

Soit M =

1) Calculer M². Vérifier que M² est de la forme M² = a M où a est un réel qu’on devra déterminer.

2) Calculer M³ et M⁴ en fonction de M et a.

3) Déduire du 2) l’expression de Mⁿ en fonction de M, a et n pour n N – {1}

1) M² = == 3 = 3 M

a = 3

2) M³ = aMM = aM² = a²M

M⁴ = M³M = a²MM = a²M² = a³M.

3) On suppose que Mⁿ = a^n-1M

Vérifions que la propriété est vraie pour n = 2

M² - a^2-1 M = aM – aM = 0

La propriété est vraie pour n = 2

On suppose la propriété vraie pour n.

Montrons qu’elle est vraie pour n+1

Mⁿ⁺¹ = Mⁿ * M = a^n-1M * M = a^n-1M² = a^n-1*aM = aⁿ*M

La propriété est vraie pour n+1 donc elle est vraie pour tout nN – {1}

Donc Mⁿ = a^n-1M

Exercice n°17

Soit A = où A et B sont des réels.

Soit I la matrice identité d’ordre 3 et J =

1) Exprimer A comme combinaison linéaire de I et J.

2) Calculer J², J³. En déduire Jⁿ pour n3.

3) En déduire A², A³, puis Aⁿ pour n3. (Pour le calcul de Aⁿ, on peut utiliser la formule de binôme de Newton qui est valable car les matrices I et J commutent.

1)= k+ jk = a et j = b

= a+ b

2) J² == J³ ==

Jⁿ = 0₃ pour n3.

3) A²=(aI)²+(bJ)²+2abIJ=a²+b²+2ab=

A³ = (aI)³ + 3a²I²bJ + 3 aIb²J² + (bJ)³ = a³+ 3a²b+3ab²

=

Donc Aⁿ =

Exercice n°18

Soit la matrice B =

1) Calculer B². Ecrire B² en fonction de B.

2) En déduire l’expression de B³, puis celle de Bⁿ pour tout entier naturel non nul.

3) Soit la matrice M = . Déterminer J telle que M = J + I₂.

4) En déduire l’expression de Mⁿ pour tout entier naturel n non nul. (Pour cela, on pourra utiliser la formule du Binôme de Newton pour les matrices qui est valable ici car I₂ et J commutent).

1) B² === 2B

B³ = 2B² = 4B

2) Bⁿ = 2^n-1B =

On veut montrer que Bⁿ = 2^n-1B =

Vérifions que la propriété est vraie pour n = 1

B¹ = 2⁰B = B =

La propriété est vraie pour n = 1.

On suppose que la propriété est vraie pour n.

Montrons qu’elle est vraie pour n+1

Bⁿ⁺¹ = Bⁿ * B = 2^n-1B * B = = = .

Donc la propriété est vraie pour n+1. Donc elle est vraie pour tout entier naturel non nul.

3) M = = J + I₂ = J +

J =- =

4) Mⁿ = (J + I₂)ⁿ =++

= + 1 +

= +

Exercice n°19

Soit C l’ensemble des matrices de la forme où a et b sont des réels.

1) Vérifier que le produit de deux matrices de C appartient à C.

2) Vérifier que, dans C, le produit est commutatif.

1) =

Le produit de ces deux matrices appartient à c avec a ka² - lb² et bab(l+k).

2) =

=

Le produit est commutatif dans C.

Exercice n°20

1) Déterminer la forme générale des matrices X qui commutent avec A =.

2) Montrer que X peut s’écrire sous la forme X = a I + b J où I est la matrice identité d’ordre 2 et J une matrice qu’on déterminera, ainsi que les constantes a et b.

3) Calculer Jⁿ pour nN*.

1).X = X.

Les matrices X qui commutent avec A sont de la forme.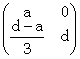

2) = aI + bJ = a+ bJ

bJ = - =

J =

a = a

b = 3(d-a)

3) J = J² = = 3J.

On veut montrer que Jⁿ = 3^n-1J.

Vérifions que la propriété est vraie pour n = 1.

J = 3⁰J = J

La propriété est vraie pour n=1.

On suppose la propriété vraie pour n.

Montrons qu’elle est vraie pour n + 1.

Jⁿ⁺¹ = Jⁿ * J = 3^n-1J * J = 3^n-1*= *.

Donc la propriété est vraie pour n + 1.

Donc elle est vraie pour tout entier positif non nul.

Exercice n°21 : matrices symétriques, antisymétriques.

1) Soient A et A’ des matrices carrées d’ordre 2. Montrer que :

^t(A + A’) = ^tA + ^tA’ ^t(^tA) = A ^t(k A) = k ^tA où k est un réel.

Montrer que ces résultats peuvent être étendus au cas où A et A’ sont des matrices carrées d’ordre quelconque.

2) Une matrice carrée est dite symétrique si elle est égale à sa transposée ; elle est dite antisymétrique si elle est égale à l’opposée de sa transposée.

Donner des exemples de matrices symétriques, antisymétriques. Donner la forme générale de ces matrices (Faire d’abord les cas 2*2, 3*3, puis passer au cas n*n).

3) Soit A une matrice carrée quelconque n*n. Que peut-on dire des matrices A + ^tA et A – ^tA ? En déduire la décomposition de A en la somme d’une matrice carrée symétrique et d’une matrice carrée antisymétrique.

Soit A = et A’ =

^t(A+A’) == ^tA+tA’ = +=

^t(^tA) == = A

^t(k A) = = k ^tA = k= .